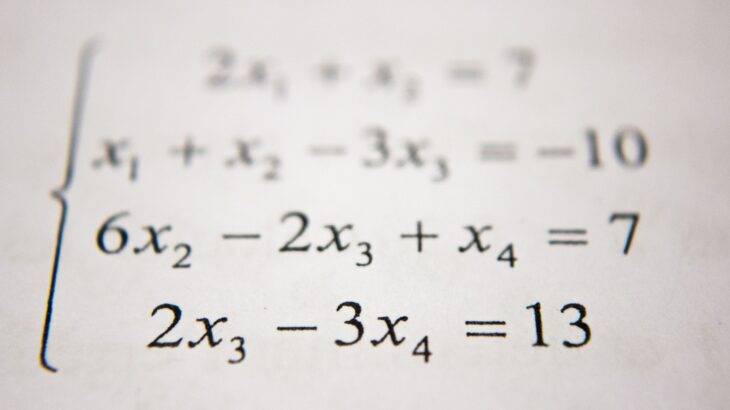勉強をしているつもりなのに、初見の問題や模試の問題が解けない
そういった悩みを持つ受験生は多いです。
この記事は、そういった人たちの参考になると思います。
力の付く数学の勉強には、1つの「型」があるのです。
数学には「解ける」の偽物がある
例えば因数分解の問題を勉強するとします。
$1+x+y+xy$
の因数分解です。
初めて勉強する問題だと想定して書いていきます。
解答を見ると
$1+x+y+xy$
$=yx+x+y+1$
$=(y+1)x+y+1$
$=(y+1)x+(y+1)$
$=(x+1)(y+1)$
となっていた。
この解答の説明では
①$x$の項と、そうでないものにわけて
②$x$について整理
③その後$y+1$という共通項でくくりだす
という「解法」が説明されていた。
これを見て、自分で解きなおすときに
①~③を思い出しながら解いた場合、それは「偽物の解ける」となります。
一見解けるようになっているようで、別な面からみると解けるようになっていません。

確かにその問題そのものは解けるようになります。
また、定期テストで少しひねられても解ける可能性は高い。
ただし。。。。
「偽物の解ける」は初見の問題や模試には使えない
模試などで次のような問題が出たとします。
$x^3-x^2y-xz^2+yz^2$を因数分解せよ。
確かに勉強した因数分解と似ています。
しかし、やや形が違って「初見」の問題です。もしくは「応用」と言ってもよいでしょう。
「解法」を思い出して
①$x$の項と、そうでないものにわけて
$x^3-yx^2-z^2x+yz^2$
②$x$について整理
$(x^2-yx-z^2)x+yz^2$
③その後・・・・?
これが初見で解けない状態のモデルケースです。
なんとなく解けている感覚
前述の勉強法の何が良くなかったのか。
勉強もして、解法も覚えていたのに解けない。
似た問題は解いたことがあり、解法もそれを使うはずなのに詰まってしまう。
解法をどのように使えばよいのか、当てはめればよいのかわからない。
定期テストでは解法が「はまっている」のに模試では「はまらない」。
なにか大事なことが「抜けている」感覚。

感じたことはありませんか。
解けても「なんとなく」解けている感覚。経験がある方も多いと思います。
そういった場合、この記事はとても参考になります。
ホントの「解ける」が身につく勉強法の場合
$1+x+y+xy$の因数分解で解法は
①$x$の項と、そうでないものにわけて
②$x$について整理
③その後$y+1$という共通項でくくりだす
というものでした。
実は、この①に入る前に大事なことがあります。
それは
「なぜ①をしようと思ったか」
ということです。
$1+x+y+xy$をみて
①$x$の項と、そうでないものにわけて・・・
そうしようと思ったのはなぜなのか。
ホントの「解ける」を身に付けている場合、こう考えることになります。
$1+x+y+xy$の式を見て
・2文字以上の因数分解の問題だ
・次数に関しては$x,y$ともに同じである。
だから
$x,y$どちらについて整理しても因数分解はできるだろうけど今回は$x$について整理しよう
そう考えた結果、①の解法が発動するのです。
模試に強い人は、自然とこういったところに意識が行く勉強法になっているはずです。
ではそういった人たちは「センス」がよいのか。
それは違います。
チャートの”指針”や”チャート”、基礎問題精講の”精講”や”ポイント”にちゃんと書かれている、
一般に、式は次数が低いほど扱いやすい。よって、複数の種類の文字を含む式の因数分解では、1つの文字、特に次数が最低の文字について整理するとよい。
というような部分をしっかりと理解して、覚えているというのがこのカラクリです。
逆に「なぜ、そのような解き方をするのか」「どういった場合にその解法となるのか」
これを軽視して具体的な解き方だけ覚えようとしている場合に、「初見の問題や、模試、実力テストに弱い」という傾向が生まれます。
それは閃きと呼ばれる
ホントの「解ける」が身につく勉強をしている場合は応用的な
$x^3-x^2y-xz^2+yz^2$を因数分解せよ。
についても、まず
・2文字以上の因数分解の問題だ
・次数に関しては$y$が最も次数が低い
だから
$y$について整理すれば因数分解はできるだろう。
そう考えて、解き始めます。
すると・・・・
$x^3-x^2y-xz^2+yz^2$を因数分解せよ。
①$y$の項と、そうでないものにわけて
$-x^2y+z^2y+x^3-xz^2$
②$y$について整理
$-(x^2-z^2)y+x^3-xz^2$
③その後その後$x^2-z^2$という共通項でくくりだす
$-(x^2-z^2)y+x(x^2-z^2)$
$=(x-y)(x^2-z^2)$
$=(x-y)(x+z)(x-z)$
こうやって「解ける」。
模試や実力テストが得意な人と、定期でしか点が出ない人の差はこれなんです。
解法を使う理由がはっきりしていて、解法がしっかり機能を果たしている。
「はまっている」感覚です。

解けない人から見ると
$y$に着目するところが「センス」があると感じる
「閃いている」と感じる
しかし、実際は”指針”や”精講”を理解し覚えているだけであることに他ならない。
センスや閃きは知識から生まれる。
ホントですよ。
ホントの「解ける」が身につく3ステップ
以上のことから数学の勉強では、無意識に抜けがちなステップがあることがわかります。
きちんと力になる勉強をするために次の3ステップが全部満たされているのか
ということ常に意識するとよいです。
①閃き
②解法
③論述
①閃き
これが問題集の”指針”や”精講”に載っている部分。
「なぜその解法をするのか」の理由にあたります。
・式の形が〇〇だから
・条件で〇〇が与えられているから
・直角三角形の斜辺の中点だから
・点Mは二等辺三角形の中点だから
・$xy$平面上で考える三角形の面積問題だから
この~だからにあたる部分が「閃き」です。
勉強しながら
「~だから」が言えるかチェックします。
②解法
この記事 でも詳しく書いていますが、抽象的に解法を暗記します。
「(閃き)だから、(解法)で答えが出る」という風に言えるかチェック。
③論述
実際に、①、②と具体的な計算式を紙に書きながら論述するステップです。
計算スピードや計算の精度も考えに含みます。
また、記述式に対応できるような解答を書けるかチェックします。
この①~③は、
①→②→③の順に重要です。
問題集はちゃんと解き進めたのに結果が出ない
問題集は解けるのに、模試では解けない
そんな悩みがある場合、この記事を参考に自己分析してみてください。