数学についてよく聞く話。

「マークは解けるけど、記述は解けない」
あるいは
「定期テストはできるけど、実力テストはできない」
この現象には共通した原因が潜んでいます。
簡単なテストで応用力は推し量れます。

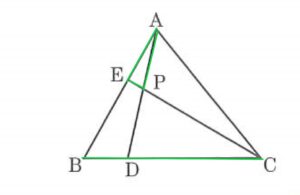
例題
上図において、$AP:PD=5:8$、$BD:DC=2:9$のとき
$AE:EB$を求めよ。
さて、答えはメネラウスの定理を使えば
$45:88$となります。
答えがあっているかは重要ではありません。
これを解いたとき
A:応用力の無い人の見え方
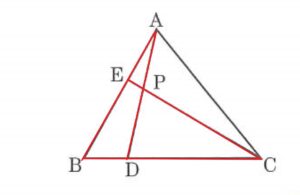
こんな風に見えて解いたのか
(三角形2個が重なって見える)
B:応用力のある人の見え方
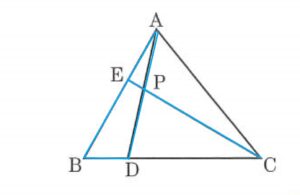
こんな風に見えて解いたのかが重要です。
(三角形一つと直線が見える)
Aの見え方をした人は次の応用問題が解けません。

例題2
上図において
$AE:EB=3:5$、$EP:PC=2:15$のとき
$AP:PD$を求めよ。
答えは$61:75$ですが、答えがあっているかは重要ではありません。
解ける人は次のように見えています。
(三角形一つと直線が見える)
応用力=目が違う
応用力のある人は、同じ問題を見ても見えている景色が違います。
問題の何をどう見ているかが違うということです。
これはわかりやすい言葉でいうと
「閃き」の差
なんだぁ、ひらめきかぁ
じゃあ結局センスの話じゃん・・・・
と思った人は、安心してください。
これはセンスのお話ではありません。
正しい「目」はだれでも養えます。
目=応用力の鍛え方
例題のタネ明かしは簡単です。
メネラウスの定理はそもそもが三角形と直線に関する定理です。
そのため、「どの三角形とどの直線に関する問題なのか」が大事なのです。
ここまで読んで意味が分からない場合は、教科書などでメネラウスの定理を確認することを勧めます。
つまりこの場合
定理を正確に理解している人=応用力がある人といえます。
このように、図形問題では
・定理の正確な理解ができてる
・定理が証明できる(全部は無理。教科書に載っている証明くらいはできるようにする)
このような人は自然と応用力の土台ができています。
数式についても同様です。
$$2x^2-xy+2y^2$$
この式をみて
・$x$の2次式だ
・$y$の2次式だ
という風に見える人もいれば
・$x$と$y$の対称式だから、$x$と$y$の基本対称式で表せる
とか
・楕円を回転させたものだ
という風に見える人もいる。
これはセンスの問題ではなく、
そういった基本問題が定着しているか
の違いです。
数学の問題の解き方
数学の問題(初見の問題)を解くときの順序は
①閃き→②解法を考える→③論理的に説明する(記述、計算する)
という順序で、どの問題でも同じ。
①の閃きについて解法を閃くときは、問題を目が見たとき脳がすでに脳に存在する
どの基本問題に似ているか、あるいは同じかをサーチして
「勝手に脳が」思い出します。
(大事。無意識なんです。だからなんで解けるのか説明するのが難しい)
つまり頭の中にその基本問題がないと閃かないということです。
記述模試や実力テスト、応用問題で手が止まる人はそこに漏れがあります。
勉強したのに閃かない
その基本問題は確かに勉強したし、解けるようになった
という実感があるのに閃かない。
そういった感想を持った人がいると思います。
そういった人は自学の際に
①閃き→②解法→③解答と勉強せずに
②解法→③解答と勉強しています。
②の解法は「作業」にあたるものです。
作業には理由が必要なんです。〇〇だから、××という作業をする。
これが正しい。
例えば「部屋が汚れているから、料理を始めよう」なんて普段の生活ではやりません。
料理も「おなかがすいた」という脳の勝手な閃きから始める作業です。
ところが数学では「なんでその解き方をするか」という着眼点(=目)を考えず
「とりあえずこう解くのだな」と解法を覚える勉強で終わる人がいます。
作業を暗記するのではなく、
①問題を見て、この問題は〇〇という特徴がある(見える)
→②だから××という解法を使う
→③そのため△△という解答になる
このように3段構成になって頭に入っているかが大事です。
今後の勉強の参考にしてください。
まとめ
数学の応用力は
①基本問題の全理解(最低でも9割以上)
②基本問題は閃き方を暗記しておく(目を鍛える)
③図形問題は定理の正確な理解と、証明の理解
の3点が大事
なぜマーク模試や定期テストは解けるのか
これらを踏まえると、なぜ定期テストやマーク模試だけ解けるのかがわかります。
マーク模試は、解法が穴埋め式で誘導されています。
つまり、問題をどのように眺めるのかの「目」が与えられている問題です。
定期テストでも、授業や宿題ですでに学校が実施した問題について
数値や問い方を少し変えるだけの出題をするので同じく
「どのように問題を眺めるのか」の目が事前に教えられた状態なのです。
そのため、「解法(作業)を覚えるのが上手」な人は得点が取れます。
しかし、問題をどう「見るか」の閃きが不足していると、途端に誘導なしでは手が止まる。
これがマーク・定期だけが点が取れる人の特徴です。
余談
数学の応用問題について、記事を書いてみました。
応用力のつけ方については記事にするのがとても難しいです。
この記事もよくわからん!っていう感想になる人もいると思います。
そのため、試験的な投稿です。
意味が分からない場合、コメント欄で質問してください。