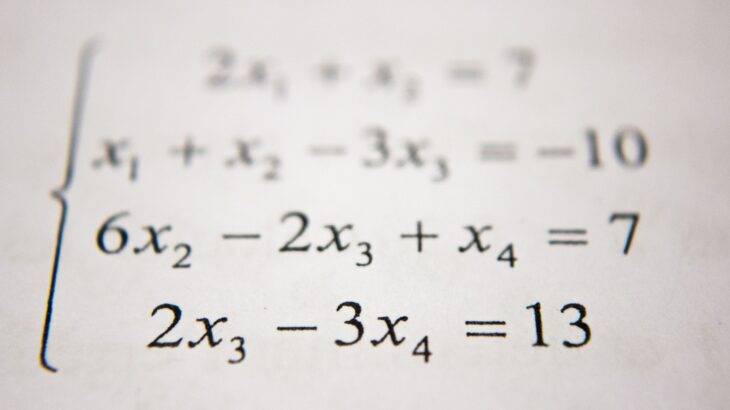比較的長めの記事です。
受験計画を考えるとき
大事になってくる考え方
スピード
大事ということはわかってても
具体的には・・・という人は必見です
超具体的に説明します
誰でもできます
今日からできます
「時速で勉強を考える」
まず、合格までの道のりをグラフで考えます

横軸は時間
縦軸は点数や偏差値です
横軸が学習量
縦軸が学習の質
ととらえてもそれほど違いはありません
志望校が同じなら、受験までの時間と合格に必要な点数は
みんな同じですから大した差がありません(重要です)
勉強は量と質だ、とかよく耳にしますよね
でもそれはライバルと同じなんです
頑張って変えられる要素ではないんです
他人が決めたものですから
もちろん勉強時間の差は結構つきます
勉強時間を1日16時間とか
もちろんそれはすごいことだしライバルに
差をつけられるでしょう
1日4時間しか勉強しない人には4倍の
8時間勉強する人には2倍の結果が期待できます
でも・・・、もっともっと
ライバルと差がつくのはグラフの傾き=スピードです
スピードの違いが圧倒的なら
時間以上にとんでもなく差がつきます
2倍とか4倍とかそういう単位ではありません
徒歩と車のレースくらいの差がつくイメージです
話を戻します
ライバルとは大体今時点で同じくらいの
順位にいる人ですからスタート地点は
たいして変わりません
グラフの縦軸と横軸はライバルと同じものを共有しているのです
グラフで考えるとき
傾きが小さければ遅く
傾きが大きければ早く
成績は変化します
合格ラインに達する時間が
かわるということです
つまり、1時間当たりどのくらい成長するか
というスピードがものを言います
どう考えてもライバルに差をつけるなら
スピードなんです
ほんとによくある失敗例
それがわかっているのに
たいていの人は受験プランを考える際
・どのテキストを(縦軸にあたる)
・何ヶ月で終わらす(横軸にあたる)
のような計画を立てると思います
時速で考えず、時間とレベルで計画しちゃうんです
さきほどいったように、それはライバルと共有している要素なので考えても仕方ないんです
まずはグラフの傾きを考えるのが大事
典型的なダメな例は
偏差値70超えたいから「青チャート」を
8月までに終わらせる
とか
偏差値60を5月までに超えたいから
4月中に基礎問精講を通る
とかいう計画です
それ、ライバルみんながやってるんじゃないですか?
私ももちろんこういう失敗の経験者です
というかこんなことばっかりやってきたので
痛いほどそのやり方の浅はかさがわかります
当時の私にアドバイスできるなら
「まずすべてやめろ、一から考え直せ」
「そんなことやるなら散歩でもして冷静に考えろ」
です
こういう計画立てるときって
とりあえず1問とか解いてみて
大問1つ書いて解くのに約10分かかる
テキスト全部で150問あるとして
(実際はⅠで170問 Aで130問くらいなので片方150問と平均にした)
10×150=1500分
1500÷60=25時間
一日2時間で2週間で1回解ける
(何回解くつもりなの?5周したら2か月かかりますよ
1周終わるころには最初の方は忘れているのでは?
ⅠAⅡBⅢとあるので1年たっても終わらないのでは?)
のように計画していくと大体の目安ができます
こうやって年間計画まで落とし込む人がいます
私も実際このように計画を立ててやっていました
しかし
この計画の立て方は絶対にうまくいきません
当たり前のことですが
問題によって10分以上かかっても
わからなかったり
やり直ししたりして
20分越えたり
5分で終わるものもあったり色々です
だから計画がおしてきて
やる気がなくなったり焦ったりします
自己否定したり、やっぱり自分は
なんて考えます
テキストが難しすぎるんだ
とか言い訳して
テキストを変えてみたり
問題が多すぎるとか考えて
抜粋して3分の1の量にしたりして
計画に合わせる・・・
いうまでもないことですが
一つのテキストの基本例題は
どのテキストでも大事なものを厳選しています
厳選されたものをさらに選別したら
確実に穴が開きます
その後のさらなる応用問で
確実に響いてきます
1冊全部やる(基本例題だけでも)
ということが単純にして大事な事なんです
テキスト変えたり
問題選別で計画は守っていても
それに伴う質(得点、偏差値、成績)はついてきません
一体何のための計画だったのか
自分の失敗を振り返ると
結局最初にちゃんと考えていないんですよ
そういう時って
みんながやっていることを
何となくなぞってみるだけ
何となく頑張ってれば受かるだろうとか
みんながやっていることをみんなより
長時間やればいいだろう
責任感ないんですよ
結果に対して
絶対合格しようという自分の発言に
絶対うまくいかせようっていう
結果に対する責任感、必死さ
ないんですよね
こういう時
「頑張れば感動」なんていうフレーズが
心の支えだったりします
「努力は実る」
実らない努力もあるんです
残念ながら
本当にこういうときってうまくいきませんよね
自分がこんなことばっかりしてたよなといつも記事を書きながら思います
話を戻しましょう
ライバルに差をつけるのに大事な傾きが
大きくなったり小さくなったりバラバラだということは
=時間内に合格ラインに達するかどうかあやふやだということ
これでは当然うまくいきません
他の人より確実に合格に早く近づく
そのために必要な考え方は
時速で計画を立てる
時速を重視する
ほとんどの受験生が気付いていない
ほとんどの先生は教えてくれない
半端なく大事な考え方なので
是非身に付けてください
わかりやすく青チャート数学を例に説明します
※私は青チャートはおすすめしませんが、使っている人、学校が異常に多いので例にしています
一つのテキストには大体
同じ難易度の問題が網羅されています
青チャートも
基本例題 はほぼ全て同じ難易度
練習問題 や exercisesは少し難しめ
なので難易度の差があまりない
基本例題だけを計画します
(グラフ傾きにぶれがなくなる)
ここで
基本例題だけやっていても
書いてはいけない、いきなり答えを見てわかるか確認する→これがなぜ大事なのかはこの記事の宿題のやり方を見てください
難しく感じたり、理解ができないものもあるでしょう
それはテキストのその問題が難しいのではなく
自分のレベルがその問題、あるいはその分野で低いということです
難易度が一定なので、自分が何をすればいいのか明確です
基本なので、難しいのではなく知らないだけ
覚えればいいだけということです
基本例題でパパっとわかるものもあれば
つまづいてわからない問題がある
そういうときに
パパっとわかる問題に合わせて計画します
とても重要なことで、これがグラフの傾きを決めます
例えば
基本例題のうちパパっとわかるものは
1分以内に問題を見て、解答を見れば
解き方が理解できるとします
途中計算とか細かいものは別に必要ありません
どういう解き方(ストーリー)なのかわかればOK
(別に2分でも3分でも構いません、自分のすでにわかる問題を処理する時間に合わせます)
この1分を基準にして
全ての問題を1分で理解するよう制限をつけます
ここでグラフの傾きが決まりました
問題が150題あれば150分ですね
2時間半で1周です
時速60題ということです
わからない問題はどうするか
1分以上かかるなら
どんどん飛ばします(一応読むことは読むけど、わからなくてよい)
解説のわからない部分にマーカーでも引いて
反復する中で何度も見ていればわかるようになります
基本例題のわからない問題は覚えていない問題です
数学的センスの問題ではありません
記憶喪失状態か
そもそも知らないかのどちらかなので
忘れているなら答えをみる
知らないなら覚えるという対処が正しい
ストップウォッチでも横に置いたりして
1分毎に鳴らします
ちゃっちゃかちゃっちゃか進みます
こうすれば2時間半で必ず1周します
絶対にできます
むしろ読み飛ばす問題もあるので2時間半より
短い時間で1周します
ありきたりな方法では25時間で1周でしたね
10倍のスピードですよ。
これが時速で立てる計画です
「考えても何分まで」ではないんです
「わかるなら1分だから、1分以上ならわからない・知らないと決めてしまいパッパとすすもう」
これが時速を上げるんです
これは計画がずれません
だってわかるわからないではなく
時間がルールなのです
2時間半で必ずチャート1冊が終わる
これって自信になりません?
周りの人が、まだ2時間半では10分の1くらいしか終わってないし
う~んとか悩んでいるのを横目に
10倍のスピードで1周しちゃってます
相当差がついてますよこの時点で
もちろんわからない問題が残ります
例えば150題中 (大げさに)70題わからないとします
そしたら2周目です
今度はわかる問題は確認程度に読み流し(一応目は通してくださいね)
わからない問題に2分くらいあてて2周目です
1周した時にある程度レベルアップしているので
1周目で分からなかったものも何個かわかるようになっています
全体を一度見ているので、どの公式が多用されているか
問題がいくつかのグループに分けられそうだ
最大・最小の問題はたいていグラフで解かれている
とか全体的なビジョンが養われはじめています
2周目も2時間半くらいでしょう
(わからない問題1問2分×70題=140分+わかる問題の確認流し読み)
この周回でもやっぱり時間をルールにして
わからないなら飛ばします
※いきなりノートに丁寧に書いて考えてはいけません
基本をやっているうちは
書いても数学の力はつきませんし時速が遅くなります
偏差値が上がらないうちは、理解して解ける状態になってから書いて解くのが大事です
理解している→書いてみるが正解なんです
わかる→書いて解いてみるが大事(この時は力がつきます)
書いてみた→わからないは時間、精神力のロスが尋常じゃないです(この記事で最重要の1文です)
計算力に関しても
計算練習は別でまとめて計算問題集とかでやった方がスピードはつきます
もちろんメモ程度にグラフを書いた方がいい問題もあるので
その辺は適宜「チラシの裏に書く程度」のイメージで書いて考えます
しかし繰り返しますが、ライバルに差をつけるとしたら
時速しかないんです!
他の時間とレベルは同じなんですから
原理原則から考えます
問題を見て解法が瞬時に出るようになってから
書いて解いてみてください
読んでわかるものは2周~3周すれば
必ず書いて解けるようになっています
3周目以降について
さらにわかるようになったものを確認
わからないものを再度考える
これは2時間もかかりません
わかる問題はどんどん増えるからです
こんな感じで5周しましょう(もちろん10周しても構いません)
一日1周として5日間です
ちなみにわかるようになった問題は3周目くらいから
問題だけを見ながら、
テストとして解法をつぶやいてください
「与式に座標をぶちこんで連立でぼーん」みたいに私はしゃべっています(3秒で復習できます)
他にも
「式を平完(平方完成のこと)してグラフ、軸の位置から区間をこれとこれとこれに場合分け、両サイド代入でぼーん、この場合だけ軸代入でぼーん」(6秒で復習)
「ぼーん」とは計算して答えを出す
ということを意味してます
単純計算なんかやらずに
省略して爆発させてやったぜ!
のイメージです(ほかでちゃんと計算ドリル的な練習はやりますよ、「合格る数学」シリーズとかおすすめ)
こうやって
テキストの8割~9割解法をしゃべれる
ようになったとします
おそらく合計10時間くらいでしょうか
(別に20時間かかってもいいですよ、1日4時間くらいなら許容範囲内です)
10時間で5周!この差はやばいです
問題を5回解いてますから
断然記憶にも残ります
1日1周として
5日間でこの成果です
その週の土日などにまとめてすべての問題を一度書いて解いてみる必要があります。
書いて解くと新たな発見・気づきがあるし、実際には計算で手こずったりするものがあるからです。
スピードを意識して「スラスラ」解けるか確認します。
(これは時間がかかります。計5時間くらいかかるかもしれません。もっとかも。でもほとんど解けるからうれしくなります)
※人によっては1日で終わらないくらいになると思うので、
実際に書いて解くのは次の週に小分けにしたりするのがおすすめです。
いわゆる一般的な計画なら
2週間で計25時間かかってたった1周、
そして解けるようになっているかわからない
時速で考える計画なら
10時間(20時間でもべつによい)で全問5周、5日で終わる
書いて確認まで入れても
15時間で全問6周以上(やり直しがあるから)、7日で終わる
そしてなにより
ほとんどすべての問題がちゃんと瞬時に解けるよう自分の力になっている
ⅠAⅡBⅢ全部やっても1か月ちょっとでにおわっちゃう!
日数で考えると、ダメな方法の半分
(7日/14日で2倍のスピード)
周回6周で6倍のスピード
ほんとの意味で解けるようになっている問題数で何倍ものスピード
計2倍×6倍×何倍も=何十倍も学習効果があるんです
あるレースをしていて
時速6キロ(頑張って早歩き)で歩いている自分の横を
時速60キロ、120キロ、180キロで走る車を見たらどうですか?
めちゃくちゃ脅威ですよね
スタートラインは同じなんですよ
スタートから早歩きの人はやる気なくしますよ
というかズルい

それくらいの時速の差でライバルをごぼう抜きにできます
是非年間計画を立てる前に参考にしてください
本当にそうなるのか疑わしいですか?
実際に勉強法の指導が終わった教室の生徒は
英語のネクステ500問を1週間に10周してきます
(※半分の250問くらいを1週間に10周にする生徒ももちろんいますよ。個人差はあります。)
数学の基礎問精講で1単元(大問20個くらい)なら1時間で平気で5周くらいします
だれでもできます
簡単とはいいませんが、できます
とにかく1度やってみることが大事
※勉強に関する相談等受け付けています
お気軽にコメントください